Concepts and Methodologies
The Department of Statistics Singapore (DOS) collects data through surveys (e.g. Household Expenditure Surveys, Price Surveys, Census, etc.) and from administrative sources (e.g. births and deaths data from the Immigration and Checkpoints Authority, education data from the Ministry of Education, Singapore, etc.).
Such data are commonly used in various forms of analyses, such as to describe or visualise patterns and trends, or to uncover relationship between variables. Learn about the common types of data, chart types typically used for data visualisation, and real-world applications of mathematical concepts such as seasonal adjustment.
Units of Analysis: Who’s in the Spotlight?
The unit of analysis refers to the entity that is being studied in a dataset. For example, in clinical trials, the unit of analysis could be an individual (i.e. the patient). Macroeconomic studies may consider a whole country as a unit of analysis, e.g. comparing the productivity of workers between countries.
Units of analysis commonly found in the data published by DOS includes:
- Individuals, on Population Structure (by Residency, Age, etc.), Marital Status, etc.
- Households, on Household Expenditure, Household Income from Work, etc.
- Firms, on Productivity, Value-added, Business Receipts Index, Retail Sales Index etc.
Types of Data: Which One Tells Your Story?
Quantitative Data versus Qualitative Data
Qualitative data are generally non-numerical which relate to words, pictures or even videos. It helps to answer ‘what’ or ‘why’ questions. An example is sentiments data which describe how individuals are feeling. Qualitative data can be analysed by grouping the data into themes or categories.
Quantitative data are numerical in nature, and help to answer questions pertaining to ‘how much’ or ‘how many’ etc. Quantitative data can be analysed using statistical analysis. Examples of quantitative data are as follows:
Cross-Sectional
- Data are collected over a single time period (e.g. records are from a specific year).
- Allows the comparison of characteristics between units or groups at a fixed point in time.
From the table below, it can be seen that in 2022, there were 6 males and 4 females. Of the 4 females, only 1 lives in HDB housing while the rest live in private estates.
Table 1: Cross sectional data of individuals in 2022 and their characteristics
| Name |
Year |
Age |
Sex |
House Type |
Highest Qualification Attained |
| Christopher |
2022 |
22 |
M |
4-Room HDB |
Diploma |
| David |
2022 |
30 |
M |
3-Room HDB |
University |
| Grace |
2022 |
40 |
F |
Condominium |
Diploma |
| Jason |
2022
|
23 |
M |
4-Room HDB |
Post-Secondary |
| John |
2022
|
55 |
M |
1-2 Room HDB |
Post-Secondary |
| Michelle |
2022
|
13 |
F |
4-Room HDB |
Below-Secondary |
| Peter |
2022 |
45 |
M |
5-Room HDB |
Bachelor's Degree |
| Sally |
2022 |
23 |
F |
Landed |
Post-Secondary |
| Samuel |
2022 |
19 |
M |
4-Room HDB |
Secondary |
| Yvonne |
2022 |
7 |
F |
Landed |
No formal qualification |
Time Series
- Data are collected at several points in time.
- Data can be collected/observed at different frequencies such as hourly, daily, weekly, monthly, quarterly, or annually.
- Ordering of records by time matters since there is a time dimension.
- Time series data allow us to identify and analyse trends or behaviours over time. Table 2 shows an upward trend in the number of individuals with higher education levels (e.g., Diploma, University) from 2017 to 2022, and a downward trend in the number of those with Secondary education or below.
- Other examples include interest rates (monthly), exchange rates (daily), GDP (annually), inflation (monthly, annual).
Table 2: Number of Singapore Residents aged 25 years and above by highest qualification attained, from 2017 to 2022
| Year |
Below secondary |
Secondary |
Post-secondary |
Diploma |
University |
| 2017 |
813,800 |
488,800 |
253,500 |
415,900 |
874,000 |
| 2018 |
761,500 |
511,200 |
260,700 |
434,900 |
908,700 |
| 2019 |
745,700 |
503,700 |
265,900 |
461,200 |
946,200 |
| 2020 |
757,800 |
484,300 |
296,900 |
456,800 |
982,000 |
| 2021 |
643,900 |
492,600 |
281,300 |
486,200 |
1,074,300 |
| 2022 |
646,300 |
492,200 |
308,000 |
521,900 |
1,116,900 |
- Combines time series and cross-sectional data, but observations in each cross section do not necessarily refer to the same unit.
- For example, individuals across the years can be randomly sampled to obtain multiple years of cross-sectional data, and these datasets can be combined together.
- The main advantage of pooled data over cross-sectional data is that the former is typically a larger sample, since multiple cross-sectional data are combined from different time periods.
Table 3: Pooled cross-sectional data of individuals from 2015 to 2022, and their characteristics
| Name |
Year |
Age |
Sex |
House Type |
Highest Qualification Attained |
| Anthony |
2017 |
22 |
M |
3-Room HDB |
Diploma |
| Anthony |
2018 |
23 |
M |
4-Room HDB |
Diploma |
| Cobalt |
2018 |
24 |
M |
4-Room HDB |
University |
| Daniel |
2019 |
30 |
M |
3-Room HDB |
University |
| Ernest |
2022 |
32 |
M |
3-Room HDB |
University |
| Felicia |
2010 |
40 |
F |
Condominium |
Diploma |
| Germaine |
2019 |
41 |
F |
Condominium |
Diploma |
| Hailey |
2015 |
45 |
F |
Condominium |
Diploma |
| Isabelle |
2022 |
13 |
F |
4-Room HDB |
Below-Secondary |
| James |
2021 |
45 |
M |
5-Room HDB |
University |
Note: Records are “pooled” into the same table. The records may be from different periods of time.
Longitudinal
- Combines cross-sectional and time series data, similar to pooled data. The difference is that the same cross-sectional units (e.g. individuals) are observed at several points in time (days, months, years, before and after event etc.). It is also known as panel data.
- Allows the observation of the same group over a period of time, and track the changes over the period. This is useful for detecting development trends or changes in the characteristics of interest. Hence, panel data are often used in studies that investigate the effects of certain events, policies or treatments. For example, the effects of a particular government policy on the wages of individuals can be studied by looking at the change in wages within individuals before and after policy implementation.
Table 4: Longitudinal data of individuals and their characteristics
| Name |
Year |
Age |
Sex |
House Type |
Highest Qualification Attained |
| Christopher |
2020 |
22 |
M |
4-Room HDB |
Diploma |
| Christopher |
2021 |
23 |
M |
4-Room HDB |
Diploma |
| Christopher |
2022 |
24 |
M |
4-Room HDB |
University |
| David |
2020 |
30 |
M |
3-Room HDB |
University |
| David |
2021 |
31 |
M |
3-Room HDB |
Post-Graduate Degree |
| David |
2022 |
32 |
M |
3-Room HDB |
Post-Graduate Degree |
| Grace |
2019 |
40 |
F |
4-Room HDB |
Diploma |
| Grace |
2020 |
41 |
F |
4-Room HDB |
Diploma |
| Grace |
2021 |
42 |
F |
Condominium |
Diploma |
| Jason |
2021 |
23 |
M |
4-Room HDB |
Post-Secondary |
| Jason |
2022 |
24 |
M |
4-Room HDB |
Post-Secondary |
| Jason |
2023 |
25 |
M |
4-Room HDB |
University |
| Michelle |
2021 |
13 |
F |
4-Room HDB |
Below-Secondary |
| Michelle |
2022 |
14 |
F |
4-Room HDB |
Below-Secondary |
| Michelle |
2023 |
15 |
F |
4-Room HDB |
Below-Secondary |
Note: Each unit (person in this example) is observed for multiple periods of time.
Primary Data vs. Secondary Data
Primary data refer to data directly collected from the data source. This can be through surveys, interviews, or experiments. Primary data are generally considered reliable and objective. However, due to limitations such as cost and complexity of data, collecting primary data may not always be possible.
Secondary data refer to data collected by another party. One drawback is that secondary data are often not tailored to accommodate the specific needs of the researcher. It may also be costly to purchase if it is not freely available to the public.
How to Analyse the Data: A Chart is Worth a Thousand Words!
Graphs and charts help to present complex data in a visually appealing and simple-to-understand manner. Learn about the common types of graphs and charts below.
Download a copy of the graphs and charts  (1 MB).
(1 MB).
Using Statistics Correctly: Can Numbers Lie?
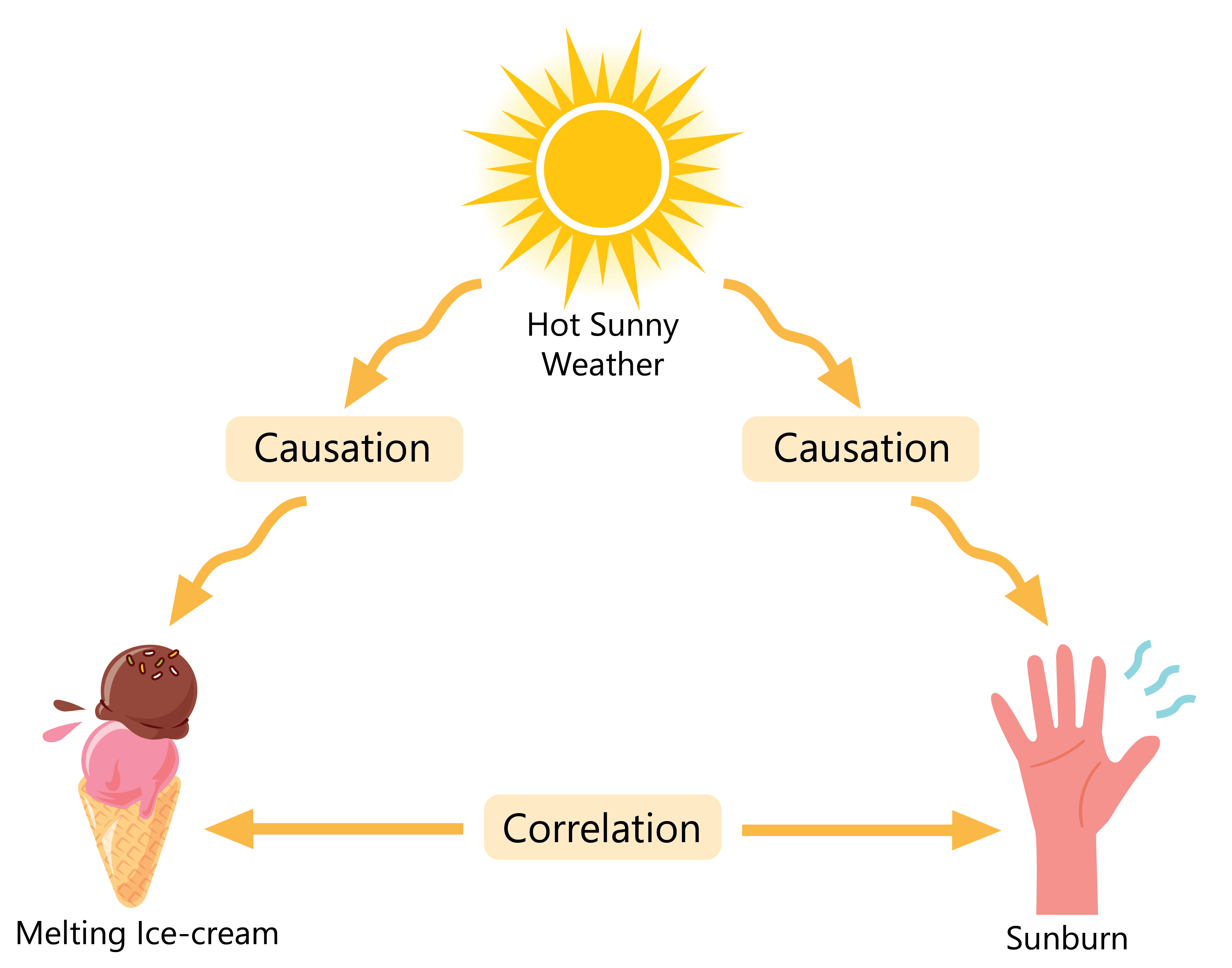
Correlation vs. Causation
Correlation is a statistical measure that indicates the extent to which the value of two or more variables move in relation to each other. Positively correlated variables tend to move in the same direction, while negatively correlated variables tend to move in opposite directions with one another. However, it may not necessarily be the case that the change in one variable causes the change in the other. On the other hand, causation means that the change in one variable causes the other variable to change.
The figure below illustrates the difference between correlation and causation. Hot sunny weather would cause an ice-cream to melt and cause sunburn (with prolonged sun exposure). Melting ice-cream and getting a sunburn are correlated, where they tend to occur together in the hot sunny weather. If the presence of the hot sunny weather was ignored, it would be wrongly concluded that melting ice-cream causes sunburn!
Difference Between Correlation and Causation
Misleading Visualisations
Authors can unknowingly produce bad visualisations of data, or worse, be out to misinform their readers. It is important to be armed with knowledge to identify bad visualisations.
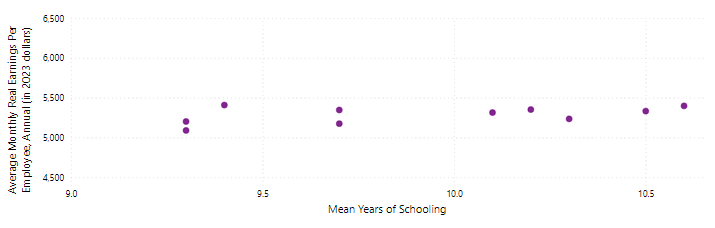
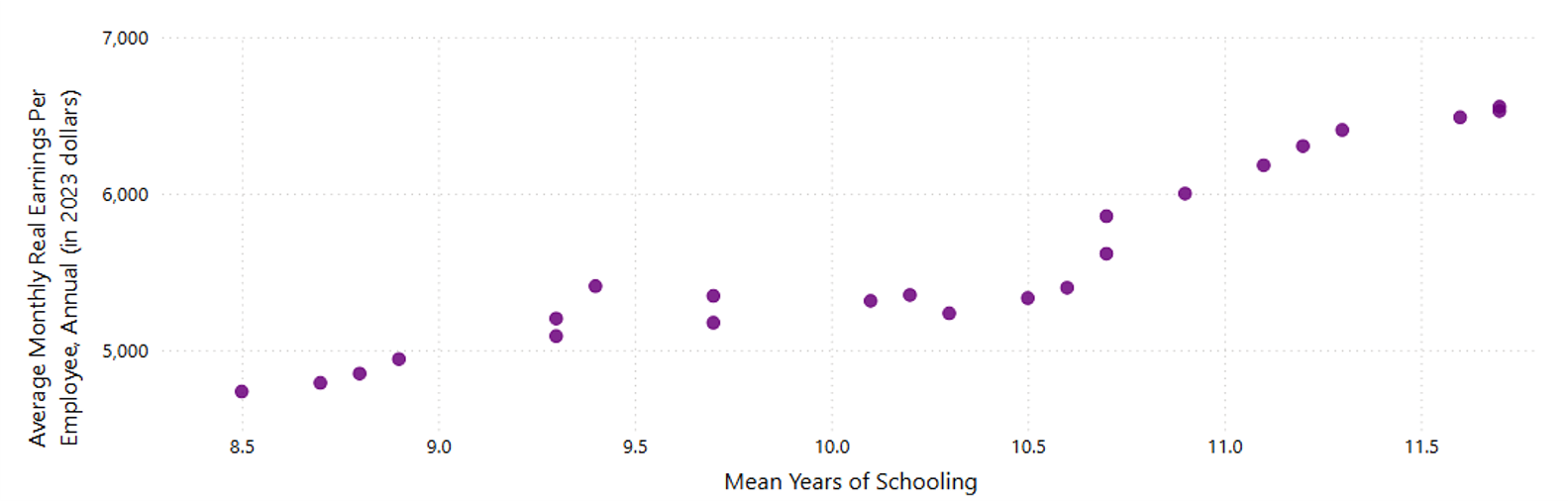
Using the chart on Average Monthly Real Earnings Per Employee against Mean Years of Schooling from the scatter plot above, data points for certain years could be omitted to give the impression that the mean years of schooling are not correlated with average real monthly income, as seen in the scatter plot below. This is known as truncated data.
Scatter plot of Average Monthly Real Earnings Per Employee against Mean Years of Schooling, with omitted data points
Scatter plot of Average Monthly Real Earnings Per Employee against Mean Years of Schooling, without omitted data points
Simpson’s Paradox
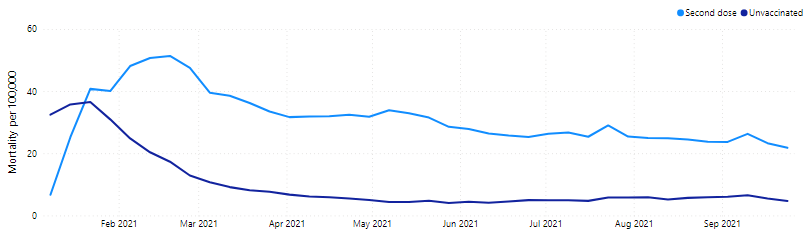
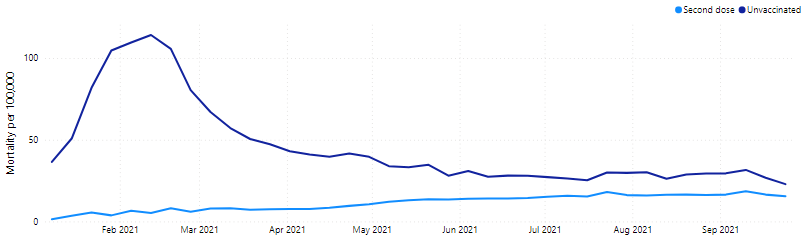
Statistics from Office for National Statistics of United Kingdom (ONS) showed that death rates for the vaccinated were greater than the unvaccinated. These numbers could be wrongly used to argue that vaccination increases the risk of death.
Simpson’s Paradox refers to the observation of a trend that is present when data are aggregated, but disappears or reverses when the groupings are made clearer (e.g. grouping by age or vaccination status). The paradox arises because death rates increase significantly with age, such that mortality rates are higher for older folks as compared to younger folks, other things being equal. Older people are more likely to be vaccinated as compared to younger people in the same age range, and are also more likely to die from Covid-19 infection or other health reasons. Therefore, age is a confounding variable since it is positively related to both vaccination rates and death rates. It is age, rather than vaccinations that is driving up the death rates of vaccinated people.
The mortality rates shown in the line chart below is a crude measure of mortality, and do not take into account the age structure of the population. Accounting for the age structure of the population is important since it can influence the number of deaths. For example, the younger population will likely have fewer deaths than the older population, all else being equal.
Mortality Rates of Individuals by Vaccination Status in UK (Jan to Sep 2021)
Instead, age-standardised mortality rates^ can be used to meaningfully compare between populations with different age structures. Age-standardised mortality rates can be computed by first calculating the mortality rates within each specified age band, followed by taking the weighted average based on a standardised age distribution.
Suppose there are 2 countries – City A and City B. City A has a younger population compared to City B but has higher mortality rate for all age bands. For simplicity, assume that there are 3 age bands – young, middle, old.
Mortality Rates of City A and City B
| City |
|
Young |
Middle |
Old |
Overall |
A
|
Mortality rate |
8% |
8% |
20% |
9.2% |
| Proportion of age group |
0.3 |
0.6 |
0.1 |
1 |
B
|
Mortality rate |
5% |
5% |
15% |
10.0% |
| Proportion of age group |
0.1 |
0.4 |
0.5 |
1 |
The unadjusted overall mortality rate in City A is 9.2% (based on (0.3 x 8%) + (0.6 x 8%) + (0.1 x 20%) = 9.2%), lower than the 10.0% of City B, even though City A’s mortality rate at each age group is higher.
Age-Standardised Mortality Rates of City A and City B
| City |
|
Young |
Middle |
Old |
Overall (Age-Standardised) |
| A |
Mortality rate |
8% |
8% |
20% |
11.6% |
| B |
Mortality rate |
5% |
5% |
15% |
8.0% |
|
Standardised Proportion of age group |
0.2 |
0.5 |
0.3 |
1 |
To do age adjustments, take the weighted average of each countries’ mortality rate using a standardised set of age group proportions in table above. In this case, the mortality rate of City A becomes 11.6% (=(0.2 x 8%) + (0.5 x 8%) + (0.3 x 20%)), and this is higher than City B’s 8.0%.
Going back to the Covid-19 vaccination example from ONS, looking at the age-standardised death rates, the death rates of vaccinated are lower than those of the unvaccinated.
Age-Standardised* Mortality Rates of Individuals by Vaccination Status in UK (Jan to Sep 2021)
^For more information on age-standardised mortality rates for Singapore, please refer to the Statistics Singapore Newsletter article (778 KB).
(778 KB).
*Age-standardised mortality rates per 100,000 people, standardised to the 2013 European Standard Population using 5-year age groups from age 10 and over.
The above information are cited from Office for National Statistics of United Kingdom (ONS) and the usage of the information is subjected to ONS's terms and conditions.
Beware of results from small sample sizes, or polls
When testing out a hypothesis, it may not always be possible to collect data for the entire population due to logistical or financial reasons (e.g. research budget). Hence, an option for researchers would be to use a smaller group, which is known as a sample (Figure 10).
Population vs Sample
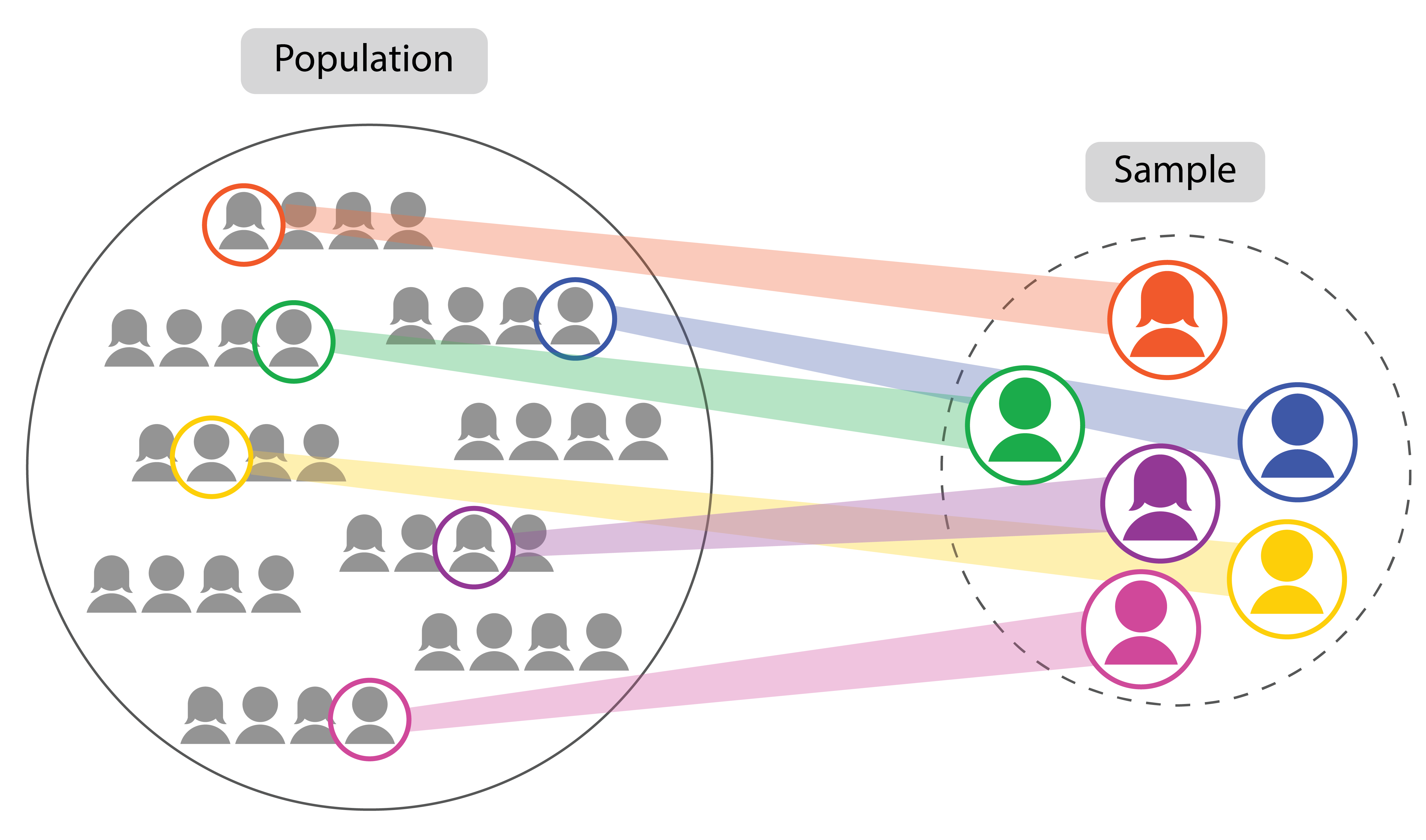
However, small sample sizes could affect the reliability of the results. One reason is because small sample sizes decrease the statistical power of a study, which means that there is a lower likelihood of detecting a true effect that exists in the entire group, via the study. Another reason could be that the sample is not representative of the population, like online polls, where only people who feel strongly about a subject would respond to the polls. This means the results are skewed towards this group of people, when the majority could be neutral about the subject. As such, robust statistical reporting or research typically requires a large enough sample size. To circumvent non-representativeness, one way is to conduct simple random sampling, where samples are chosen strictly by chance, so that all members of the population have the same chance of being selected for the study.
Concluding Remarks
As statistics is a broad field, the content above above serves as a brief and simple introduction to the different types of data, ways to analyse data, and the common pitfalls of using statistics. With this new-found knowledge, enjoy exploring and working with data to gain useful insights.